积分器中的噪声
代表采样输入参考噪声，这部分噪声包含输入的开关管和OTA的噪声。
: 代表由OTA产生的参考输出的噪声，不包含采样噪声。
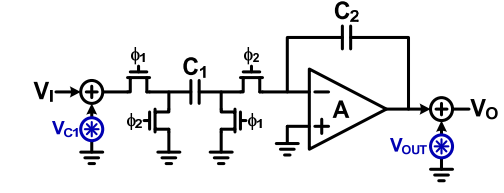image-20210929164933232
首先，OTA的热噪声，对于单端输出的OTA
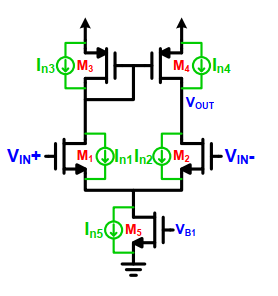image-20210929165034025
每一个晶体管都会产生一个电流噪声源 , 这里假设
假设两个路径完全匹配，所以M5不贡献差分信号的噪声。M1和M2的噪声比较容易，可以直接计算出这两个管子对于输入的参考噪声为 . 而对于M3和M4而言，输入的参考噪声为。所以，总的输入参考噪声为 其中 取决于放大器的结构。
当把这样一个OTA接到一个电容回路中，如下图所示
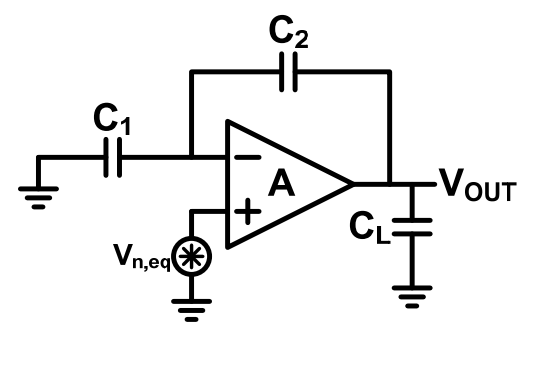image-20211006141147360
整个闭环系统的传输函数为 其中G是DC增益，假设放大器的增益远大于反馈系数时 是电路的主极点，如果电路采用的单极放大器 如果采用的是两级放大器结构 其中为补偿电容。
综上，整个系统的在输出端噪声可以表示为 $$ $$ 我们可以看出，整个系统的噪声不再取决于。
当系统的热噪声被采样，存在以下几个特性
1 总噪声维持不变
2 噪声发生混叠，从高频噪声混叠入低频噪声，如下图。
3 噪声功率谱密度将会明显增加。
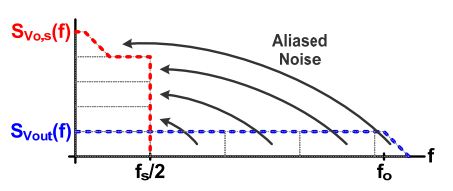image-20211006143635857
相同的噪声面积，但是经过采样后，0到fs/2的噪声功率谱密度将会明显增加。 低频的噪声功率谱密度将会由原来的增长为原来得 倍。 是这个系统的建立时间，是两相位时钟的建立时间。
在设计的时候需要满足 其中，所以PSD至少增加倍。如果N=10, PSD增加7.6 或8.8dB。
所以这是对于一个采样系统相对于连续系统的一个隐含的缺点。
对于下面的开关电容积分器
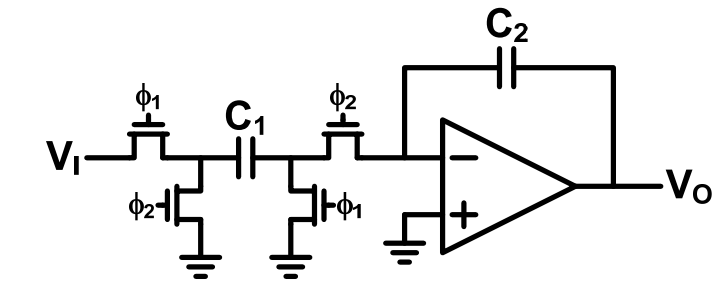image-20211008111957864
我们需要分别考虑两个相位的噪声: 采样相位和积分相位
1 采样相位
噪声包含所对应的开关的噪声。
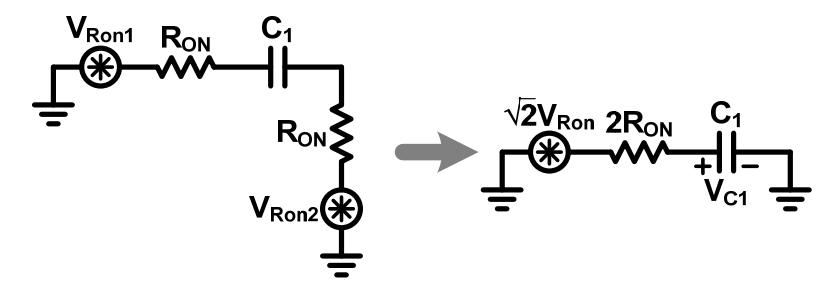image-20211008150622688
噪声主要来源于两个开关的噪声 整个电路可以等效为一阶低通滤波器，中间存在一个极点。极点对应的时间常数为 所以由于开关电阻产生的噪声加载在的两端的噪声电压为 由于积分是在整个频谱的积分 可以看出采样相位的噪声和的大小没有关系，但是与系统前端的时间常数中的的大小成反比。
2 积分相位
噪声包含OTA的噪声和所对应的开关噪声。
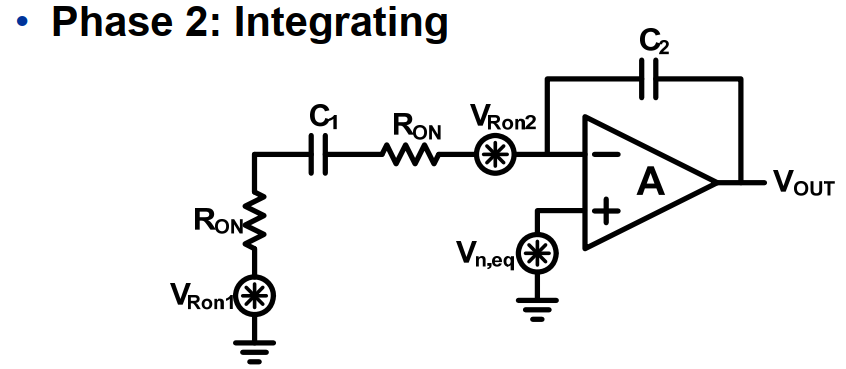image-20211008154414296
这里存在两个噪声来源：开关和OTA
两个开关产生的噪声为 由之前的计算可知，OTA产生的噪声为 上的噪声由以上两个一起产生
需要计算噪声的大小，必须计算这个电路的时间常数。而在这个电路中，电容的另外一端接了一个OTA。
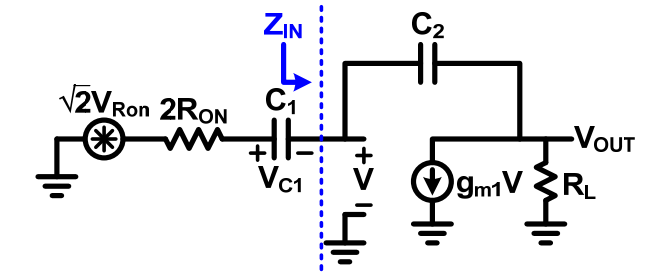image-20211008155146975
其中由电容的右端向OTA输入端看过去的等效输入阻抗为 由于我们需要足够高的增益~60dB，所以一般来说比较大。这里输入信号是一个包含DC低频信号，C2一般为pF级。忽略C2带来的影响 所以时间常数为 所以在积分相位中，由OTA产生的噪声为 由开关产生的噪声为 其中
所以整个开关电容的噪声为 $$ $$ 如果时，可以达到最小的噪声。
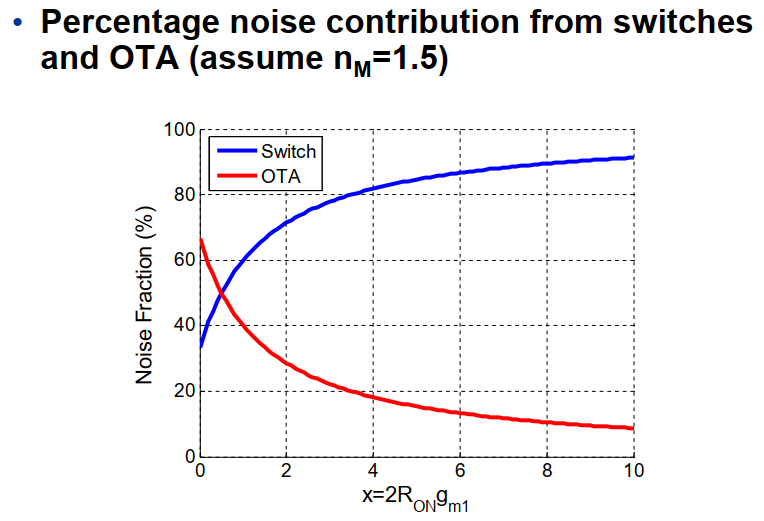image-20211008162249394
从图中得知，当x增大时，开关的噪声逐渐成为主要的噪声源，这也与直觉相符合，x增大一般来源于着增大，将会贡献更多的噪声。但是系统的总噪声会随着的增大而减小，主要是因为增大使得串联电路的时间常数增加，从而造成带宽的减小，使得系统总噪声减小。
当时，这也是我们常用的情况，主要由OTA主导整个噪声，当固定建立时间和噪声大小的时候，存在最小的值，使得系统的功耗最低。这里假设时间常数由积分阶段限制，所以 可以推出的值为， 所以对于x越小，的值也越小。而，所以可以用较小的值，实现相同的时间常数和噪声特性。而基于反相器结构的放大器，，由PMOS和NMOS同时提供， 所以功耗能更低。
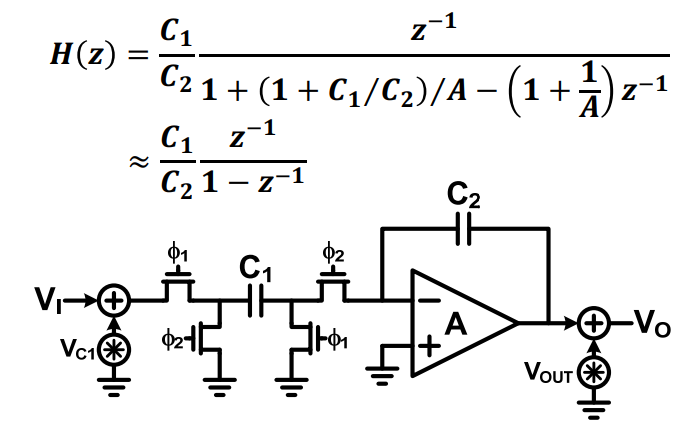image-20211008185040267
在应用中，我们时固定信号得带宽，通常情况下需要知道每个频率点噪声功率谱密度，而上图得传输函数为 而总得输出参考噪声功率谱密度PSD，可以如下表示 其中 由于所有的噪声都经过采样而产生噪声折叠，对于白噪声的功率谱密度可以表示为
其中NTF表示为
如果采用多输入端口的开关电容积分器
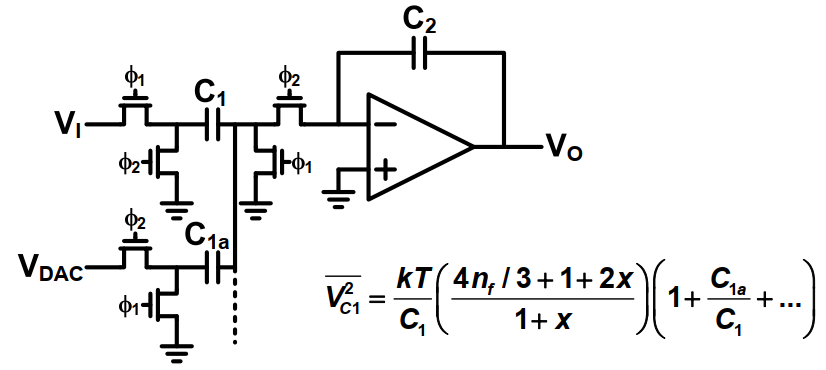image-20211008173944267
明显可以看出，加入的开关电容，使得电容两端的噪声又有了额外的噪声源，从而使得两端的噪声增加。
考虑其他电容影响
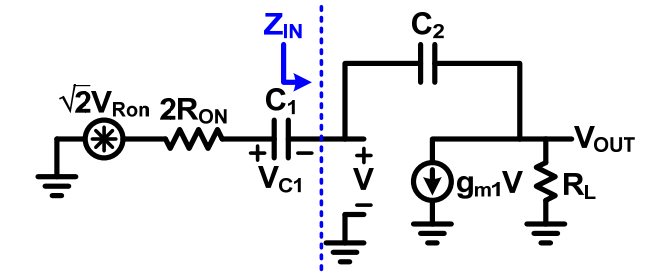image-20211008155146975
当不能忽略C2电容的时候，OTA和反馈电容等效输入阻抗为 所以噪声源到C1两端的传递函数为，而其中Cp电容相对于米勒等效电容可以忽略不记。 由于 考虑寄生电容很大的情况 所以，只要满足，或者，
所以开关电容电路的噪声主要与相关，而与其相连的寄生电容影响较小，从等式上看，寄生电容的增大，能使得时间常数稍稍增加。
