Linear Feedback Shift Registers (LFSRs)

LFSR Analysis Circuit Design
Circuit
发布日期:   2021-07-22
更新日期:   2022-04-03
文章字数:   1.5k
阅读时长:   9 分

A linear feedback shift register is a combination of series of flip flop and XOR or XNOR logic gates. It is an important component in communication system where, it paly important role in various application such as cryptography application, CRC generator and checker circuit, gold code generator, for generation of pseudorandom sequence, for designing encoder and decoder in different communication channels to ensure network security. [1]

image-20210722170537967

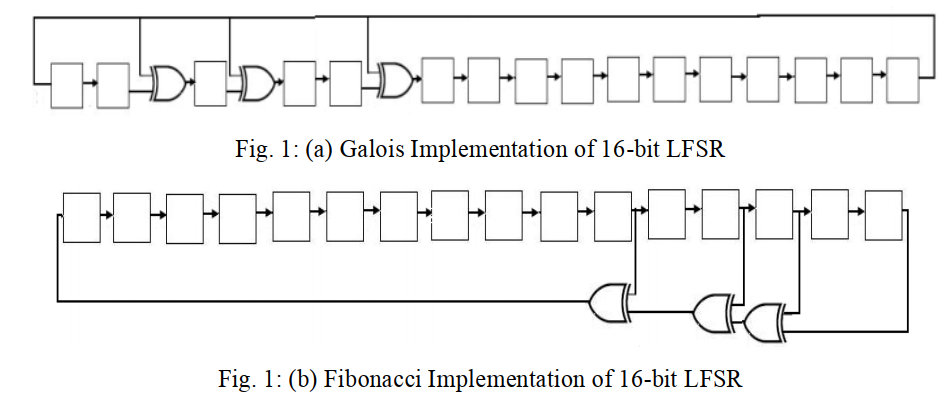
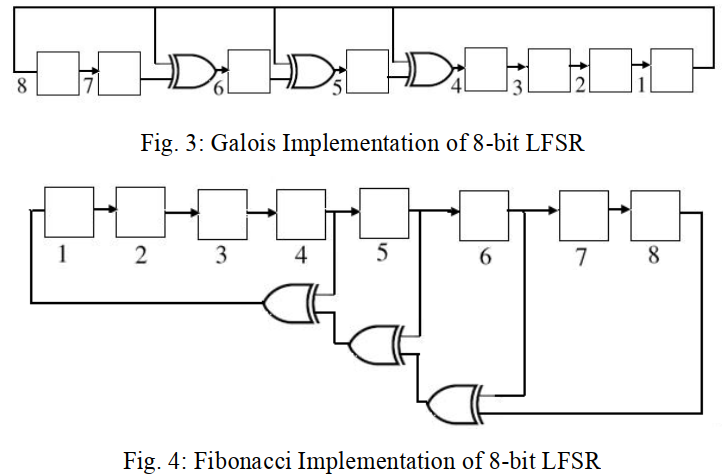
LFSR can be implemented in two styles- Galois implementation and Fibonacci implementation. The Galois or in-line or modular type implementation of LFSR having XOR gates in between shift registers. In Fibonacci or out-of line or simple type implementation, XOR gates are placed in the feedback path. In Galois and Fibonacci implementation of LFSR the fate flow direction is from left to right and right to left is the direction of the feedback path. But in Galois implementation feedback path is from MSB to LSB of LFSR while in Fibonacci implementation it is from LSB to MSB of LFSR.

image-20210722171310733

The feedback polynomial can be used to describe their feedback property. If we choose . The tap position is [8, 6, 5, 4, 1].

image-20210722172418894

With a initial state [0,1,1,1,0,0,1,1], the period can be achieved 2^8-1=255. In addition, the feedback polynomial is primitive polynomial.

import numpy as np 
from pylfsr import LFSR #[2]
state = [0,1,1,0,0,0,1,1]
fpoly = [8,6,5,4]
L = LFSR(initstate=state,fpoly=fpoly)
result = L.test_properties(verbose=2)
8 bit LFSR with feedback polynomial  x^8 + x^6 + x^5 + x^4 + 1
Expected Period (if polynomial is primitive) =  255
Current :
 State        :  [0 1 1 0 0 0 1 1]
 Count        :  0
 Output bit   :  -1
 feedback bit :  -1
1. Periodicity
------------------
 - Expected period = 2^M-1 = 255
 - Pass?:  True

2. Balance Property
-------------------
 - Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) =  (128, 127)
 - Pass?:  True

3. Runlength Property
-------------------
 - Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
 - Runs:  [64 32 16  8  4  2  1  1]
 - Pass?:  True

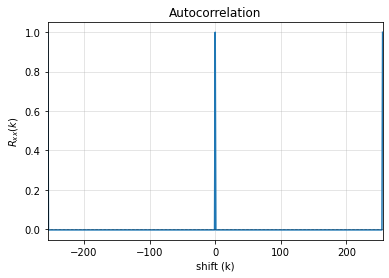
4. Autocorrelation Property
-------------------
 - Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
 - Rxx(k):  [ 1.         -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157  1.         -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157 -0.00392157
  1.        ]
img 
 - Pass?:  True



==================
Passed all the tests
==================
image-20210723221527569

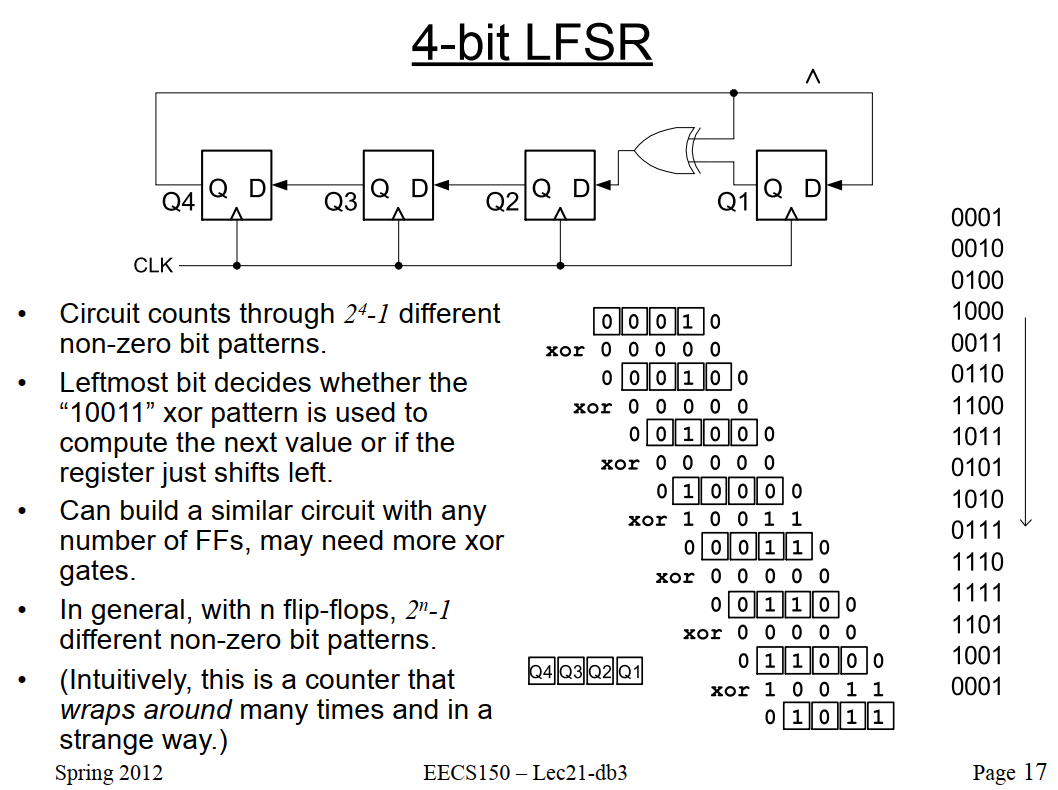
We can achieve pseudo-random codes from a LFSR, as shown in flowing figure. Leftmost bit decides whether the "10011" XOR pattern is used to compute the next value or if the register just shifts left.

image-20210722193429960

In addition, it can be used to check the data consistency.

image-20210722195359179

[1] Mishra, S., Tripathi, R. R., & Tripathi, D. K. (2016, March). Implementation of configurable linear feedback shift register in VHDL. In 2016 International Conference on Emerging Trends in Electrical Electronics & Sustainable Energy Systems (ICETEESES) (pp. 342-346). IEEE.

[2] https://github.com/Nikeshbajaj/Linear_Feedback_Shift_Register

文章作者: elike
文章链接: https://elike-ypq.github.io/2021/07/22/2021-07-22-linear-feedback-shift-registers-lfsr3/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 elike !
LFSR Analysis Circuit Design
评论
 上一篇
Superconducting quantum processor Superconducting quantum processor
A major milestone along the way is the demonstration of quantum computational advantage, which is known as quantum supremacy. It is defined by a quantum device that can implement a well-defined task overwhelmingly faster than any classic computer to an extent that no classical computer can complete the task within a reasonable amount of time.
2021-07-27 quantum processor
Superconducting quantum processor Example
下一篇 
Thermal Noise of Switch Capacitor Circuits Thermal Noise of Switch Capacitor Circuits
2021-07-11 Circuit Noise
Analysis Circuit Design Switch Capacitor